2.1 初级排序算法
2.1.2 选择排序
不断地选择剩余元素之中的最小者
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| public class Selection {
public static boolean less(Comparable v, Comparable w) { return v.compareTo(w) < 0; }
private static void exch(Comparable[] a, int i, int j) {
Comparable t = a[i]; a[i] = a[j]; a[j] = t;
}
public static void sort(Comparable[] a) { // 将a[]按升序排列
int N = a.length; // 数组长度
for (int i = 0; i < N; i++) { // 将a[i]和a[i+1..N]中最小的元素交换
int min = i; // 最小元素的索引
for (int j = i + 1; j < N; j++)
if (less(a[j], a[min])) min = j;
exch(a, i, min);
}
}
}
|
2.1.3 插入排序
将其余所有元素在插入之前都向右移动一位
1
2
3
4
5
6
7
8
9
10
11
12
| public class Insertion
{
public static void sort(Comparable[] a)
{ // 将a[]按升序排列
int N = a.length;
for (int i = 1; i < N; i++)
{ // 将 a[i] 插入到 a[i-1]、a[i-2]、a[i-3]...之中
for (int j = i; j > 0 && less(a[j], a[j-1]); j--)
exch(a, j, j-1);
}
}
}
|
2.1.6 希尔排序
基于插入排序的快速的排序算法,使数组中任意间隔为h的元素有序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| public class Shell
{
public static void sort(Comparable[] a)
{ // 将a[]按升序排列
int N = a.length;
int h = 1;
while (h < N/3) h = 3*h + 1; // 1, 4, 13, 40, 121, 364, 1093, ...
while (h >= 1)
{ // 将数组变为h有序
for (int i = h; i < N; i++)
{ // 将a[i]插入到a[i-h], a[i-2*h], a[i-3*h]... 之中
for (int j = i; j >= h && less(a[j], a[j-h]); j -= h)
exch(a, j, j-h);
}
h = h/3;
}
}
}
|
2.2 归并排序
将两个有序的数组归并成一个更大的有序数组
2.2.1 原地归并的抽象方法
将两个不同的有序数组归并到第三个数组中
1
2
3
4
5
6
7
8
9
10
11
| public static void merge(Comparable[] a, int lo, int mid, int hi)
{ // 将a[lo..mid] 和 a[mid+1..hi] 归并
int i = lo, j = mid+1;
for (int k = lo; k <= hi; k++) // 将a[lo..hi]复制到aux[lo..hi]
aux[k] = a[k];
for (int k = lo; k <= hi; k++) // 归并回到a[lo..hi]
if (i > mid) a[k] = aux[j++];// 左半边用尽取右半边
else if (j > hi ) a[k] = aux[i++];// 右半边用尽取左半边
else if (less(aux[j], aux[i])) a[k] = aux[j++];// 右半边小于左半边取右半边
else a[k] = aux[i++];// 右半边大于等于左半边取左半边
}
|
2.2.2 自顶向下的归并排序
如果它能将两个子数组排序,它就能够通过归并两个子数组来将整个数组排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| public class Merge
{
private static Comparable[] aux; // 归并所需的辅助数组
public static void sort(Comparable[] a)
{
aux = new Comparable[a.length]; // 一次性分配空间
sort(a, 0, a.length - 1);
}
private static void sort(Comparable[] a, int lo, int hi)
{ // 将数组a[lo..hi]排序
if (hi <= lo) return;
int mid = lo + (hi - lo)/2;
sort(a, lo, mid); // 将左半边排序
sort(a, mid+1, hi); // 将右半边排序
merge(a, lo, mid, hi); // 归并结果(代码见“原地归并的抽象方法”)
}
}
|
2.2.3 自底向上的归并排序
先归并那些微型数组,然后再成对归并得到的子数组
1
2
3
4
5
6
7
8
9
10
11
12
13
| public class MergeBU
{
private static Comparable[] aux; // 归并所需的辅助数组
// merge()方法的代码请见“原地归并的抽象方法”
public static void sort(Comparable[] a)
{ // 进行lgN次两两归并
int N = a.length;
aux = new Comparable[N];
for (int sz = 1; sz < N; sz = sz+sz) // sz子数组大小
for (int lo = 0; lo < N-sz; lo += sz+sz) // lo:子数组索引
merge(a, lo, lo+sz-1, Math.min(lo+sz+sz-1, N-1));
}
}
|
2.3 快速排序
是一种分治的排序算法。它将一个数组分成两个子数组,将两部分独立地排序
快速排序和归并排序是互补的
- 归并排序:分成两个子数组分别排序,并将有序的子数组归并以将整个数组排序。递归调用发生在处理整个数组之前。一个数组被等分为两半
- 快速排序:当两个子数组都有序时整个数组也就自然有序了。递归调用发生在处理整个数组之后 。切分(partition)的位置取决于数组的内容
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| public class Quick
{
private static void sort(Comparable[] a, int lo, int hi)
{
if (hi <= lo) return;
int j = partition(a, lo, hi); // 切分
sort(a, lo, j-1); // 将左半部分a[lo .. j-1]排序
sort(a, j+1, hi); // 将右半部分a[j+1 .. hi]排序
}
private static int partition(Comparable[] a, int lo, int hi)
{ // 将数组切分为a[lo..i-1], a[i], a[i+1..hi]
int i = lo, j = hi+1; // 左右扫描指针
Comparable v = a[lo]; // 切分元素
while (true)
{ // 扫描左右,检查扫描是否结束并交换元素
while (less(a[++i], v)) if (i == hi) break;
while (less(v, a[--j])) if (j == lo) break;
if (i >= j) break;
exch(a, i, j);
}
exch(a, lo, j); // 将v = a[j]放入正确的位置
return j; // a[lo..j-1] <= a[j] <= a[j+1..hi] 达成
}
}
|
2.3.3 算法改进
2.3.3.1 切换到插入排序
2.3.3.2 三取样切分
2.3.3.3 熵最优的排序
适用于含有大量重复元素的数组。将数组切分为三部分,分别对应小于、等于和大于切分元素的数组元素
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| public class Quick3way
{
private static void sort(Comparable[] a, int lo, int hi)
{
if (hi <= lo) return;
int lt = lo, i = lo+1, gt = hi;
Comparable v = a[lo];
while (i <= gt)
{
int cmp = a[i].compareTo(v);
if (cmp < 0) exch(a, lt++, i++);
else if (cmp > 0) exch(a, i, gt--);
else i++;
} // 现在 a[lo..lt-1] < v = a[lt..gt] < a[gt+1..hi]成立
sort(a, lo, lt - 1);
sort(a, gt + 1, hi);
}
}
|
2.4 优先队列
删除最大元素和插入元素
2.4.1 API
| public class MaxPQ <Key extends Comparable> | |
|---|
| MaxPQ() | 创建一个优先队列 |
| MaxPQ(int max) | 创建一个初始容量为 max 的优先队列 |
| MaxPQ(Key[] a) | 用 a[] 中的元素创建一个优先队列 |
| void Insert(Key v) | 向优先队列中插入一个元素 |
| Key max() | 返回最大元素 |
| Key delMax() | 删除并返回最大元素 |
| boolean isEmpty() | 返回队列是否为空 |
| int size() | 返回优先队列中的元素个数 |
2.4.3 堆的定义
当一棵二叉树的每个结点都大于等于它的两个子结点时,它被称为堆有序
二叉堆:一组能够用堆有序的完全二叉树排序的元素,并在数组中按照层级储存(不使用数组的第一个位置)
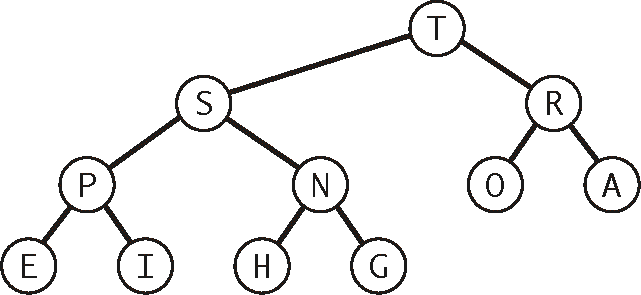
2.4.4 堆的算法
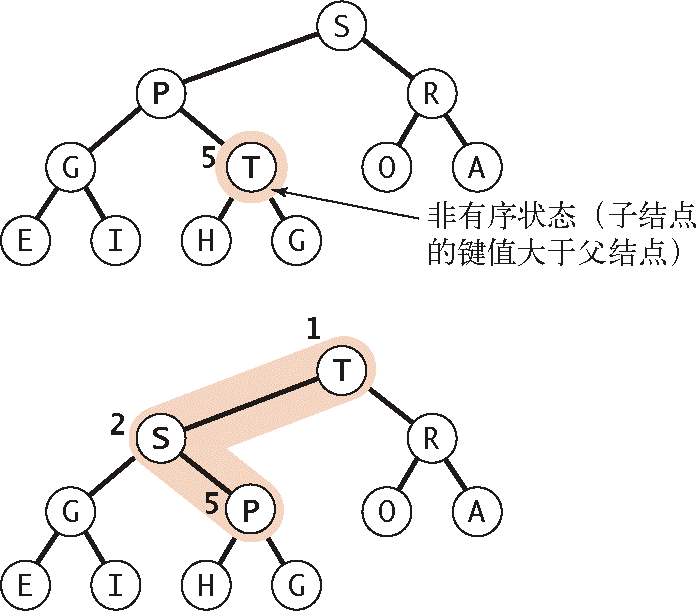
上浮:当某个结点的优先级上升(或是在堆底加入一个新的元素)
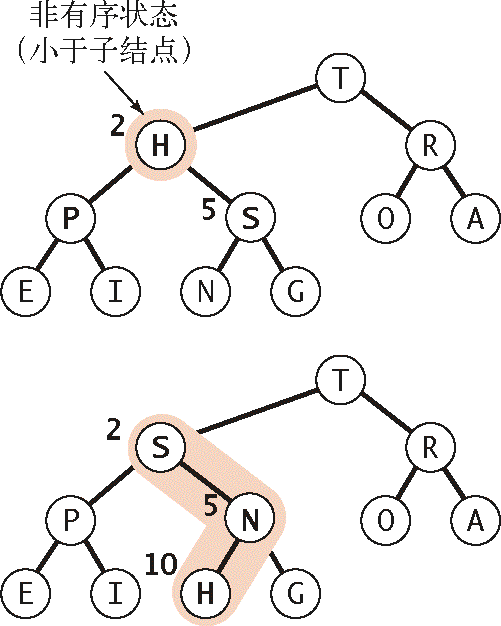
下沉:当某个结点的优先级下降(例如,将根结点替换为一个较小的元素)
2.4.4.1 由下至上的堆有序化(上浮)
1
2
3
4
5
6
7
8
| private void swim(int k)
{
while (k > 1 && less(k/2, k))
{
exch(k/2, k);
k = k/2;
}
}
|
2.4.4.2 由上至下的堆有序化(下沉)
1
2
3
4
5
6
7
8
9
10
11
| private void sink(int k)
{
while (2*k <= N)
{
int j = 2*k;
if (j < N && less(j, j+1)) j++;
if (!less(k, j)) break;
exch(k, j);
k = j;
}
}
|
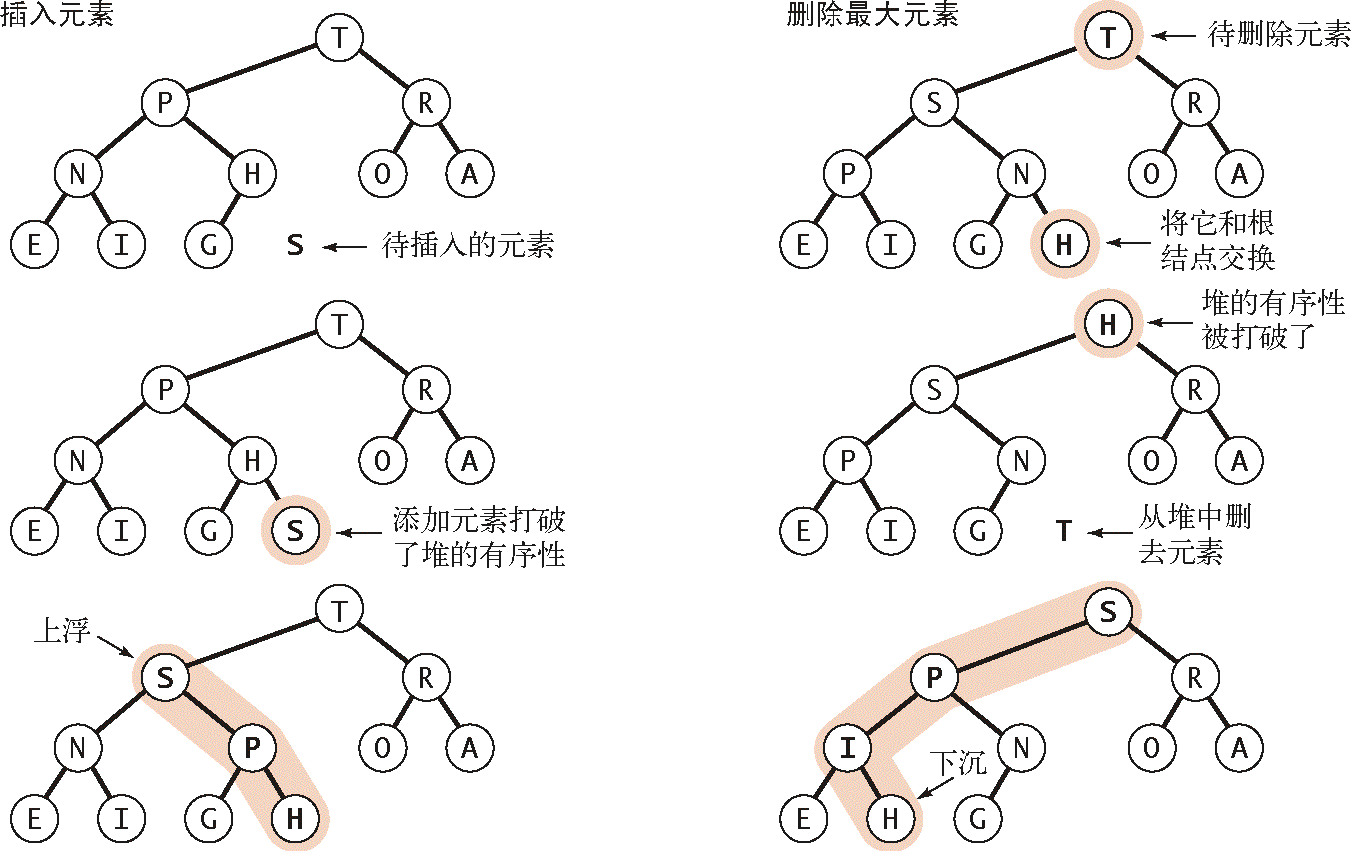
插入元素:将新元素加到数组末尾,增加堆的大小并让这个新元素上浮到合适的位置
删除最大元素:从数组顶端删去最大的元素并将数组的最后一个元素放到顶端,减小堆的大小并让这个元素下沉到合适的位置
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| public class MaxPQ<Key extends Comparable<Key>>
{
private Key[] pq; // 基于堆的完全二叉树
private int N = 0; // 存储于pq[1..N]中,pq[0]没有使用
public MaxPQ(int maxN){ pq = (Key[]) new Comparable[maxN+1]; }
public void insert(Key v)
{
pq[++N] = v;
swim(N);
}
public Key delMax()
{
Key max = pq[1]; // 从根结点得到最大元素
exch(1, N--); // 将其和最后一个结点交换
pq[N+1] = null; // 防止对象游离
sink(1); // 恢复堆的有序性
return max;
}
}
|
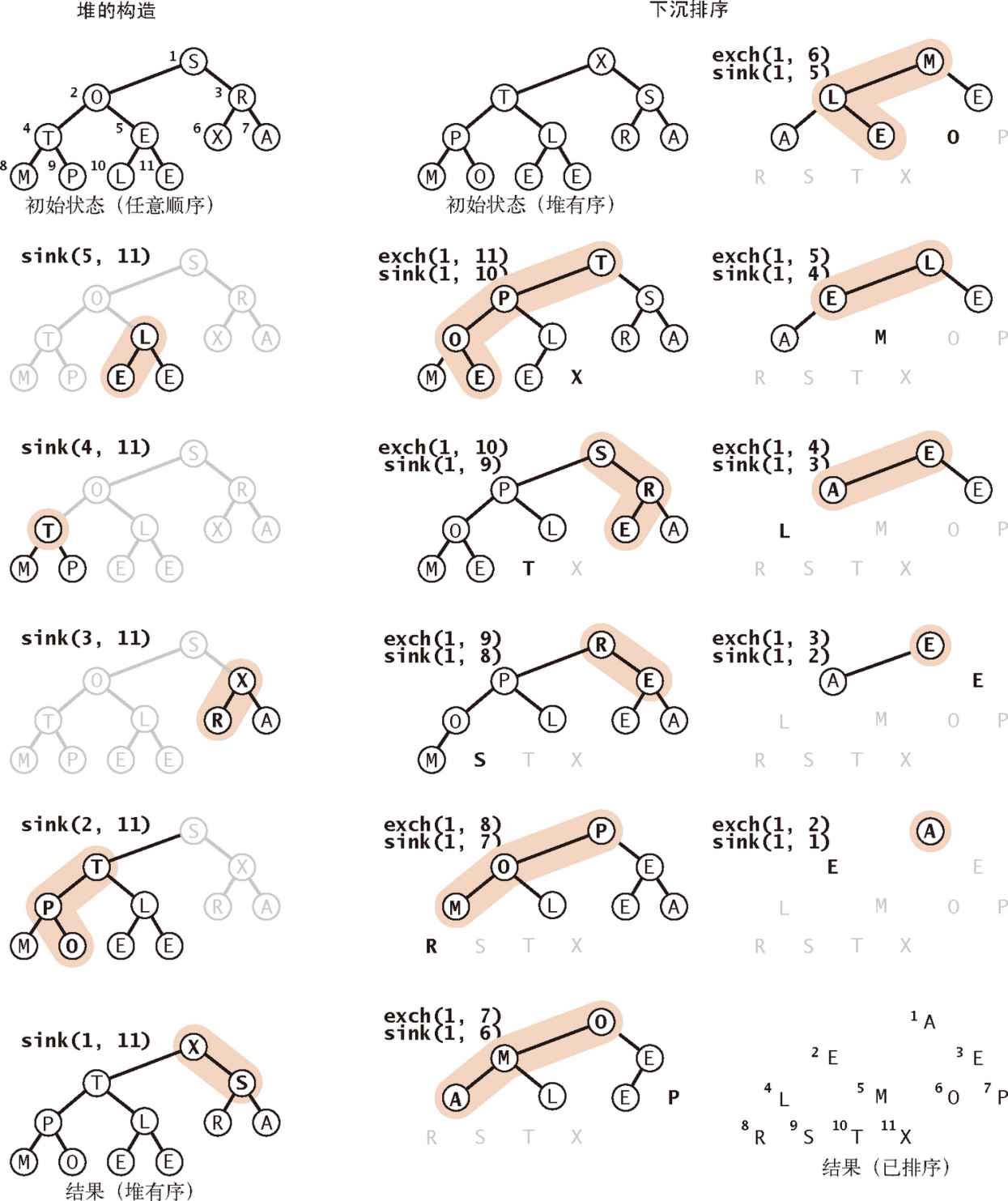
2.4.5 堆排序
1
2
3
4
5
6
7
8
9
10
11
| public static void sort(Comparable[] a)
{
int N = a.length;
for (int k = N/2; k >= 1; k--)
sink(a, k, N);
while (N > 1)
{
exch(a, 1, N--);
sink(a, 1, N);
}
}
|
文章作者
lim
上次更新
2026-01-07
(589ac56)
许可协议
CC BY-NC-ND 4.0





