权值(树中所有边的权值之和)最小的生成树
- 加权图:为每条边关联一个权值或是成本的图模型
- 图的生成树:含有其所有顶点的无环连通子图
4.3.1 原理
4.3.1.1 切分定理
将图的所有顶点分为两个非空且不重叠的两个集合。横切边是一条连接两个属于不同集合的顶点的边
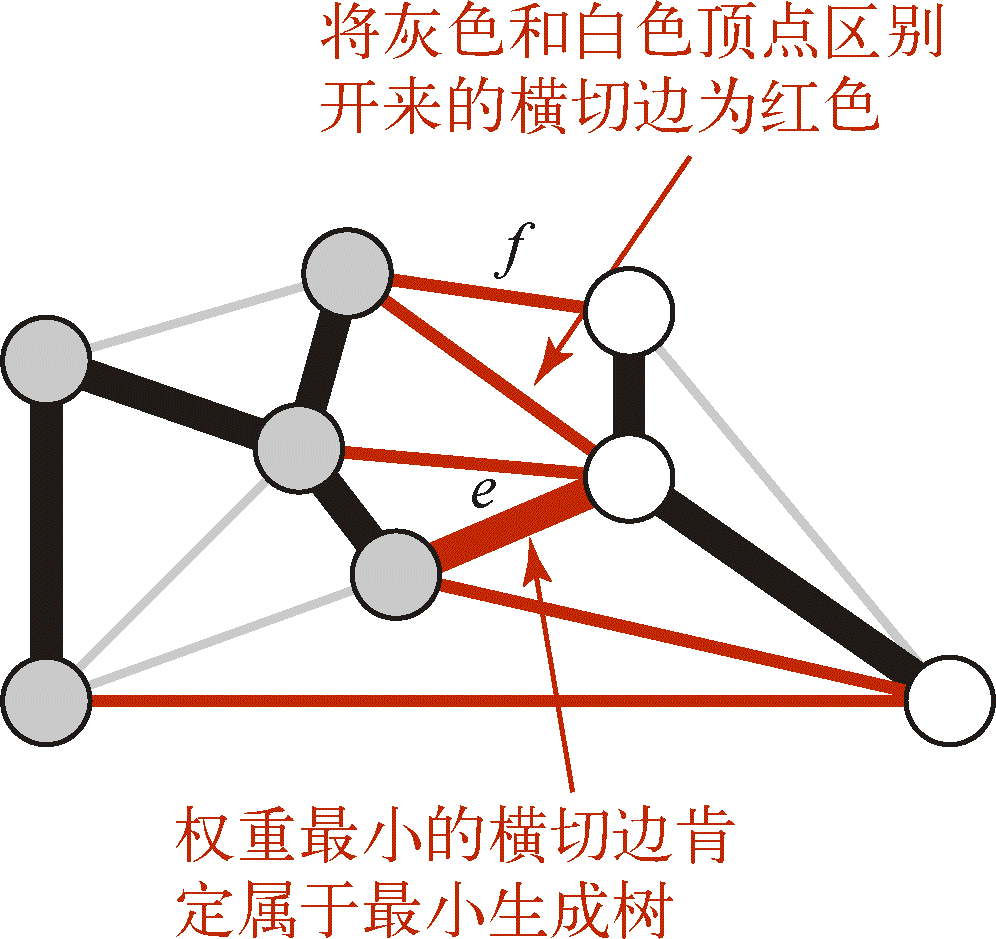
4.3.1.2 贪心算法
使用切分定理找到最小生成树的一条边,不断重复直到找到最小生成树的所有边
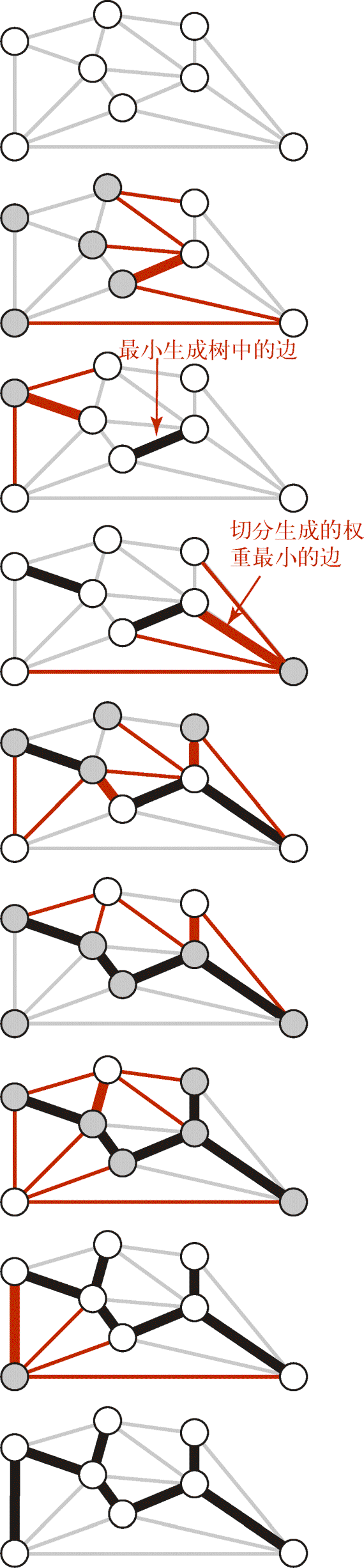
4.3.2 加权无向图的数据类型
| public class Edge implements Comparable | |
|---|
| Edge(int v, int w, double weight) | 用于初始化的构造函数 |
| double weight() | 边的权重 |
| int either() | 边两端的顶点之一 |
| int other(int v) | 另一个顶点 |
| int compareTo(Edge that) | 将这条边与 that 比较 |
| String toString() | 对象的字符串表示 |
| public class EdgeWeightedGraph | |
|---|
| EdgeWeightedGraph(int V) | 创建一幅含有 V 个顶点的空图 |
| EdgeWeightedGraph(In in) | 从输入流中读取图 |
| int V() | 图的顶点数 |
| int E() | 图的边数 |
| void addEdge(Edge e) | 向图中添加一条边 e |
| Iterable adj(int v) | 和 v 相关联的所有边 |
| Iterable edges() | 图的所有边 |
| String toString() | 对象的字符串表示 |
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
| public class Edge implements Comparable<Edge>{
private final int v;//顶点之一
private final int w;//另一个顶点
private final double weight;//边的权重
public Edge(int v,int w,double weight){
this.v=v;
this.w=w;
this.weight=weight;
}
public double weight(){return weight;}
public int either(){return v;}
public int other(int vertex){
if(vertex==v)return w;
else if(vertex==w)return v;
else throw new RuntimeException("Inconsistent edge");
}
public int compareTo(Edge that){
if(this.weight()<that.weight())return -1;
else if(this.weight()>that.weight())return +1;
else return 0;
}
public String toString(){ return String.format("%d-%d %.2f",v,w,weight);}
}
public class EdgeWeightedGraph{
private final int V;//顶点总数
private int E;//边的总数
private Bag<Edge>[] adj;//邻接表
public Edge Weighted Graph(int V){
this.V = V:
this.E = 0;
adj = (Bag<Edge>[]) new Bag[V];
for(int v=0;v<V;v++)
adj[v]=new Bag<Edge>();
}
public EdgeWeightedGraph(In in)
public int V(){return V;}
public itn E(){return E;}
public void addEdge(Edge e){
int v= e.either(),w=e.other(v);
adj[v].add(e);
adj[w].add(e);
E++;
}
public Iterable<Edge> adj(int v){return adj[v];}
public Iterable<Edge> edges(){
Bag<Edge> b = new Bag<Edge>();
for (int v = 0; v < V; v++)
for (Edge e : adj[v])
if (e.other(v) > v) b.add(e);
return b;
}
}
|
4.3.3 最小生成树的 API 和测试用例
| public class MST | |
|---|
| MST(EdgeWeightedGraph G) | 构造函数 |
| Iterable edges() | 最小生成树的所有边 |
| double weight() | 最小生成树的权重 |
4.3.4 Prim 算法
每一步都会为一棵生长中的树添加一条边
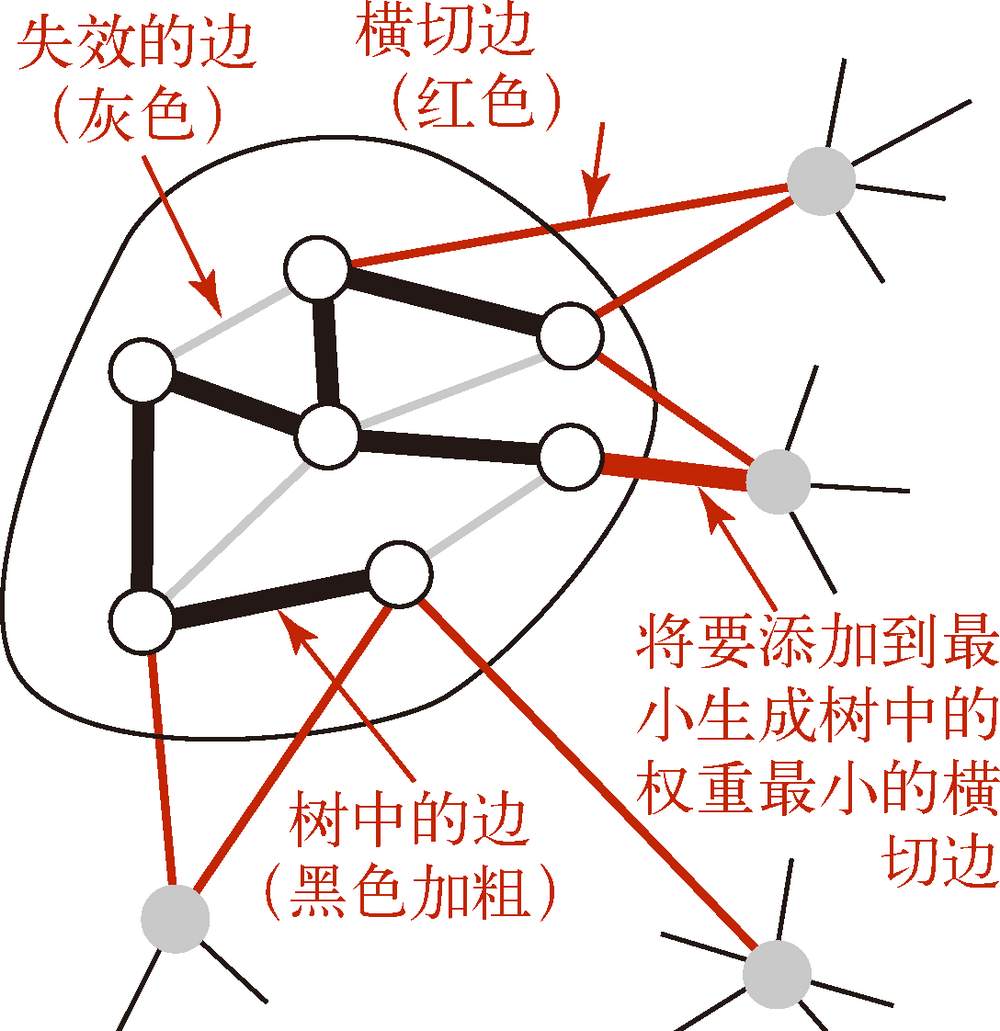
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| public class LazyPrimMST{
private boolean[] marked; // 最小生成树的顶点
private Queue<Edge> mst; // 最小生成树的边
private MinPQ<Edge> pq; // 横切边(包括失效的边)
public LazyPrimMST(EdgeWeightedGraph G){
pq = new MinPQ<Edge>();
marked = new boolean[G.V()];
mst = new Queue<Edge>();
visit(G, 0); // 假设G是连通的
while (!pq.isEmpty())
{
Edge e = pq.delMin(); // 从pq中得到权重最小的边
int v = e.either(), w = e.other(v);
if (marked[v] && marked[w]) continue; // 跳过失效的边
mst.enqueue(e); // 将边添加到树中
if (!marked[v]) visit(G, v); // 将顶点(v或w)添加到树中
if (!marked[w]) visit(G, w);
}
}
private void visit(EdgeWeightedGraph G, int v){
// 标记顶点v并将所有连接v和未被标记顶点的边加入pq
marked[v] = true;
for (Edge e : G.adj(v))
if (!marked[e.other(v)]) pq.insert(e);
}
public Iterable<Edge> edges(){ return mst; }
public double weight()
}
|
4.3.5 Prim 算法的即时实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| public class PrimMST{
private Edge[] edgeTo; // 距离树最近的边
private double[] distTo; // distTo[w]=edgeTo[w].weight()
private boolean[] marked; // 如果v在树中则为true
private IndexMinPQ<Double> pq; // 有效的横切边
public PrimMST(EdgeWeightedGraph G){
edgeTo = new Edge[G.V()];
distTo = new double[G.V()];
marked = new boolean[G.V()];
for (int v = 0; v < G.V(); v++)
distTo[v] = Double.POSITIVE_INFINITY;
pq = new IndexMinPQ<Double>(G.V());
distTo[0] = 0.0;
pq.insert(0, 0.0); // 用顶点0和权重0初始化pq
while (!pq.isEmpty())
visit(G, pq.delMin()); // 将最近的顶点添加到树中
}
private void visit(EdgeWeightedGraph G, int v){ // 将顶点v添加到树中,更新数据
marked[v] = true;
for (Edge e : G.adj(v)){
int w = e.other(v);
if (marked[w]) continue; // v-w失效
if (e.weight() < distTo[w]){
// 连接w和树的最佳边Edge变为e
edgeTo[w] = e;
distTo[w] = e.weight();
if (pq.contains(w)) pq.change(w, distTo[w]);
else pq.insert(w, distTo[w]);
}
}
}
public Iterable<Edge> edges()
public double weight()
}
|
4.3.6 Kruskal 算法
按照边的权重顺序(从小到大)处理它们,将边加入最小生成树中,加入的边不会与已经加入的边构成环,直到树中含有V-1条边为止
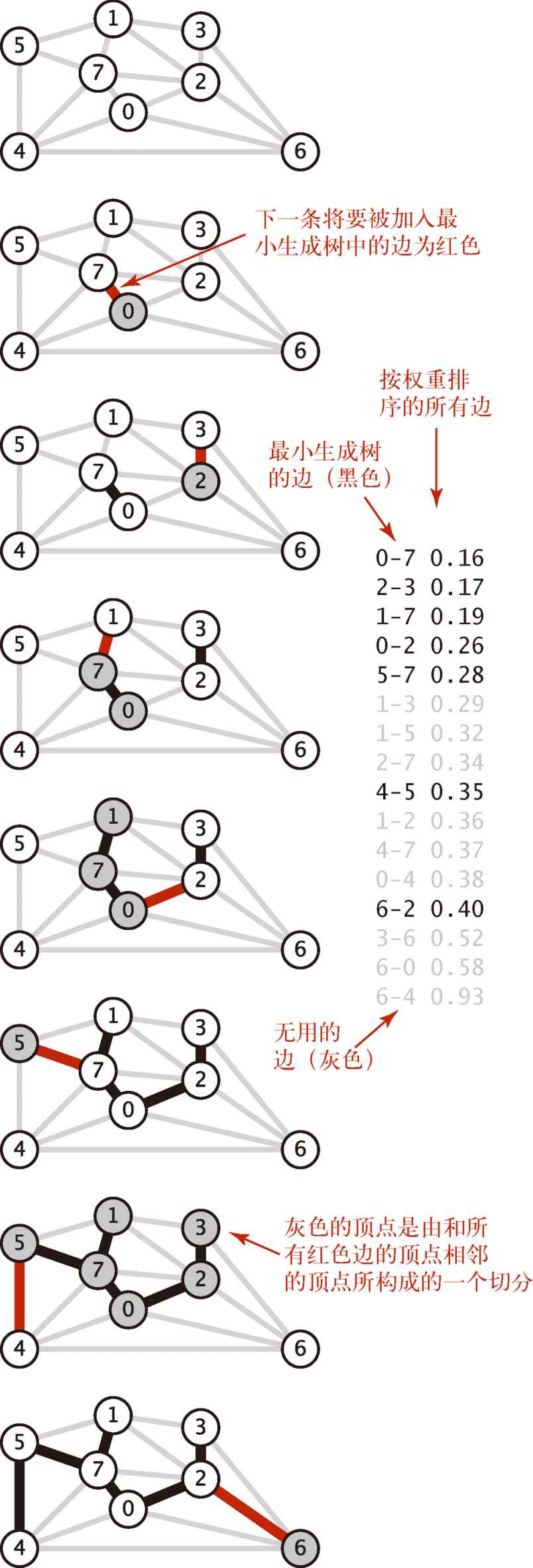
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| public class KruskalMST{
private Queue<Edge> mst;
public KruskalMST(EdgeWeightedGraph G){
mst = new Queue<Edge>();
MinPQ<Edge> pq = new MinPQ<Edge>();
for(Edge e:G.edges()) pq.insert(e);
UF uf = new UF(G.V());
while (!pq.isEmpty() && mst.size() < G.V()-1){
Edge e = pq.delMin(); // 从pq得到权重最小的边和它的顶点
int v = e.either(), w = e.other(v);
if (uf.connected(v, w)) continue; // 忽略失效的边
uf.union(v, w); // 合并分量
mst.enqueue(e); // 将边添加到最小生成树中
}
}
public Iterable<Edge> edges(){ return mst; }
public double weight()
}
|
文章作者
lim
上次更新
2024-09-14
(2aae67a)
许可协议
CC BY-NC-ND 4.0




